Welcome to the workshop. This is part 2 of the functional programming with JavaScript series.
In this part, we will learn about Currying in Functional Programming. If you haven’t gone through part-1 then I strongly recommend checking it out first.
This workshop should take around 25 minutes to complete.
Prerequisites
The workshop is for anyone familiar with:
- Javascript
- How to run a Node.js program
- General programming concepts

You don't need to be a Guru in these topics, a basic understanding of them is more than enough!
Workspace
Fork It :-
I will be using repl.it as my workspace for this workshop, You can fork my repl from here.
Nah! would do it myself (:
Or you can setup your own repl, make sure you create a node.js repl, and install the ramda package ( not rambda, because it too exists! )
Search Ramda
search for ramda in repl, make sure you don't search rambda ( because it too exists! ).
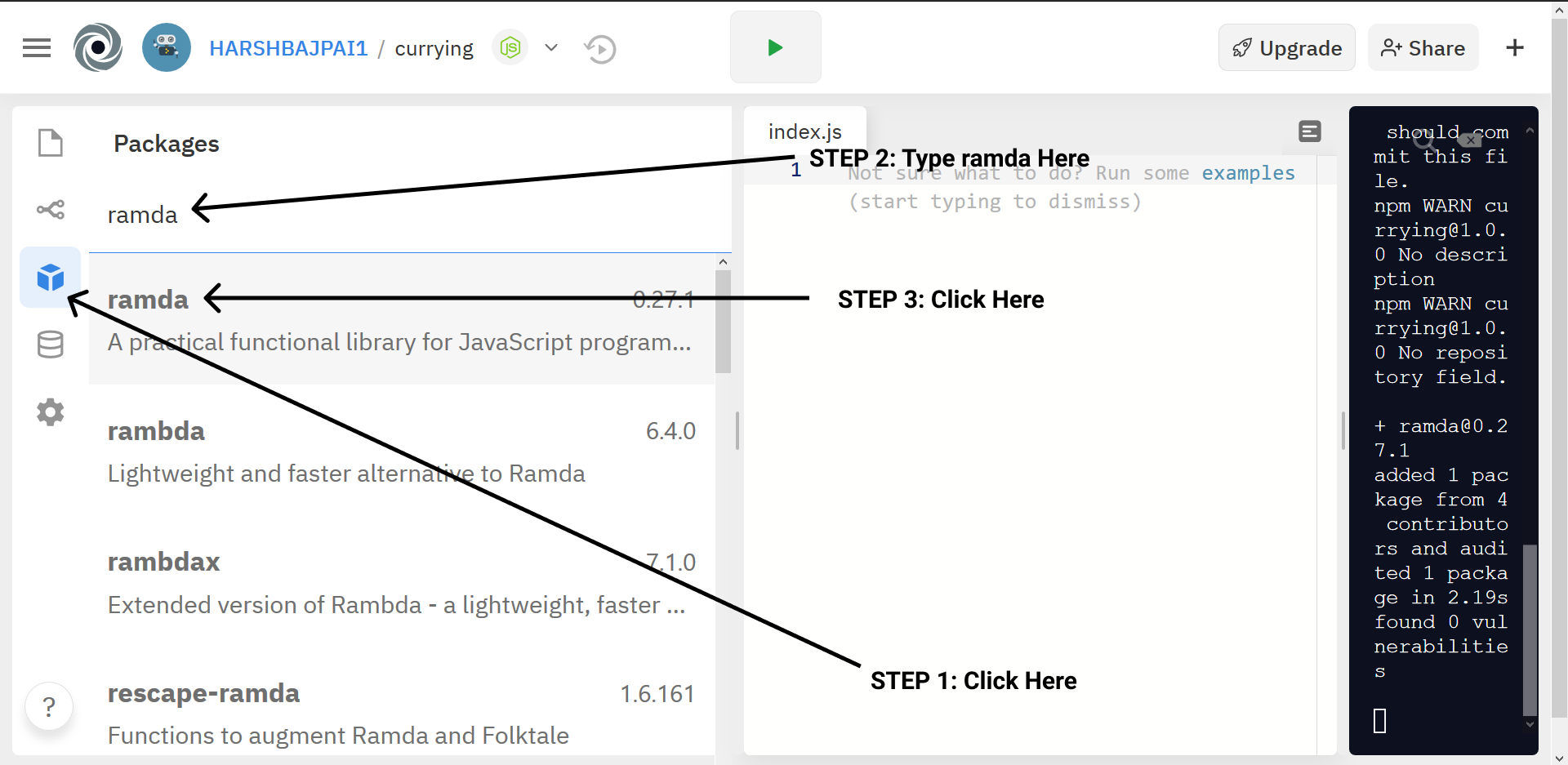
Install It
Now, install it! Click the Run button to run your program.
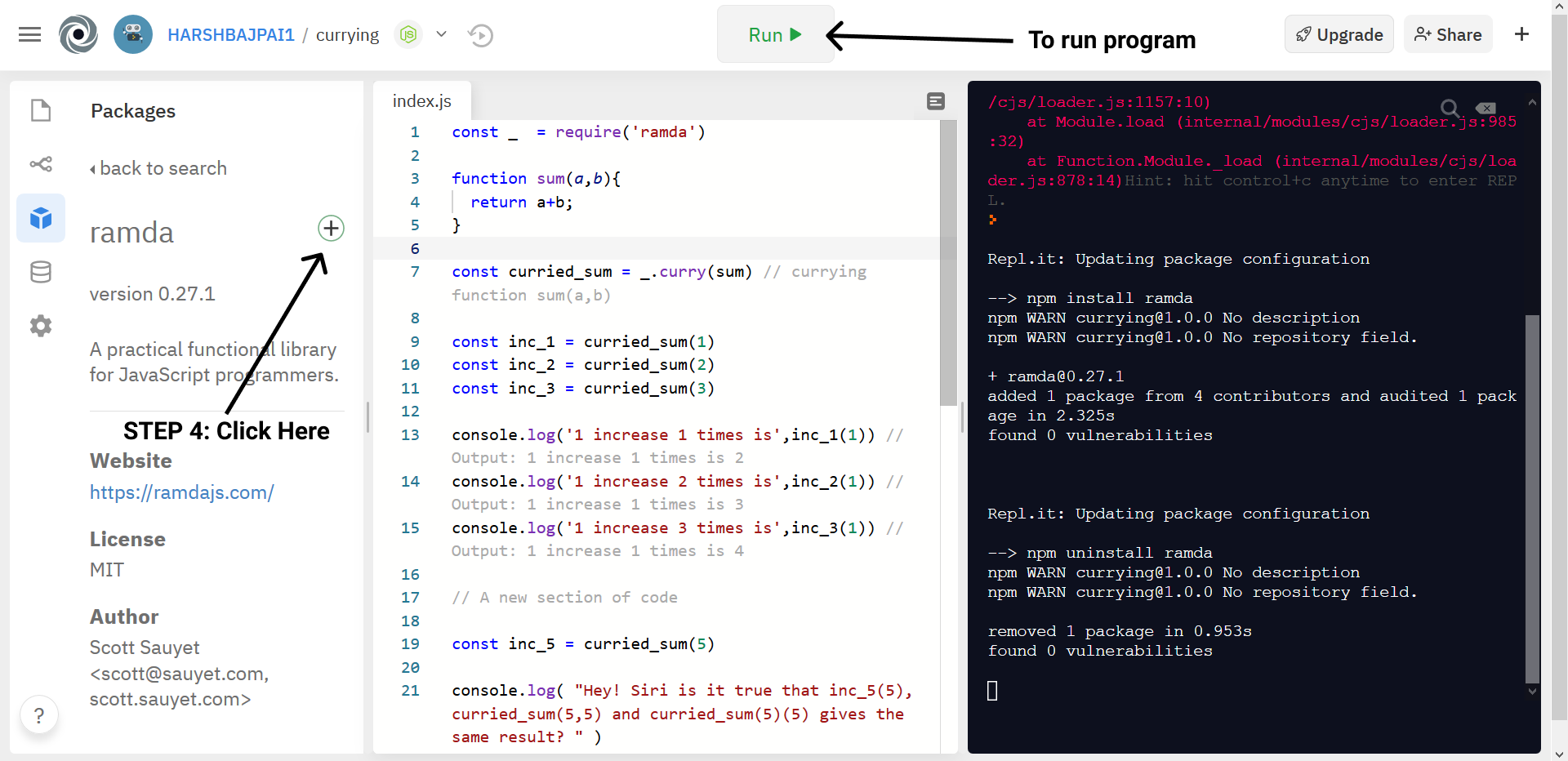
If you prefer to work offline, then install ramda via
npm install ramda
Hello Ramda!
So, we have already discussed Ramda in our first part. We will use its pre-built functions to implement functional programming. No one wants to re-invent the wheel ( although some people might! ) and wants to make the car instead.

The same goes here, we are leveraging the pre-built functions from Ramda to boost our development process!
Currying = Yummy-Yummy-Yum-Yum!
Lol! Don’t focus much on the Yummy-Yummy-Yum-Yum part, if after reading the section you find it funny, then it was written by purpose and if not then It was just a typo!

So, what is Currying in Functional Programming, Is it related to cooking? Let me answer that for you!
Currying is a core part of writing code via the functional paradigm. It helps us transform a function of form f(a,b,c) to f(a)(b)(c). Sounds confusing right?

Let me explain this with a simple example! This example will give you a practical insight into what currying is for.
Suppose you have a function sum(a,b), it takes two numbers and add them and then returns the result. This is what it will look like:
function sum(a,b){
return a+b;
}
console.log(“The sum of 5 and 2 is”, sum(5, 2))
// Output:- The sum of 5 and 2 is 7
Hmm, So this was simple! Where is the real challenge? Okay! So, what if I tell you to create three functions which would increase the value of a number by 1,2, and 3 respectively. This is what you might come up with as a solution:
function inc_1(a){
return a+1;
}
function inc_2(a){
return a+2;
}
function inc_3(a){
return a+3;
}
console.log(‘1 increased 1 times is’,inc_1(1)) // Output: 1 increased 1 times is 2
console.log(‘1 increased 2 times is’,inc_2(1)) // Output: 1 increased 1 times is 3
console.log(‘1 increased 3 times is’,inc_3(1)) // Output: 1 increased 1 times is 4
You see the problem here inc_1, inc_2, and inc_3 all three of them are doing the same thing, i.e all of them are basically the addition of a number with different values, but we already have a function sum(a,b) for that remember.

So, If somehow we could use this function sum(a,b) to create all three of these functions then how awesome it could be. The problem is that sum(a,b) expects two values as its parameters.
Okay, so let’s think about how can we overcome this limitation.
Maybe, we need this?
What we need is a way so that we could transform our sum(a,b) function into a function, which when provided a single input a, would return a new function, this new function must already have the earlier passed value to add ( i.e a ) so that it can basically add whatever number we pass to it to a. ( meaning b+a ).
Hmm, still confusing? Okay, let me simplify!

In short, we need something like this:
inc_a = sum(a) // here inc_a is a new function
inc_a(b) // adds b to a , i.e b+a
But, the question is how do we get a function like this? This is where currying comes into play!
Here comes the savior!
Okay, so we have a function curry in Ramda, which lets us do exactly this. Okay, just be with me here and go through the below example, after that things will be more clear, which finally will help us to understand the concept of currying! ( I don’t want to rush to the theoretical explanation without going through a practical scenario ).

The same inc_1,inc_2, and inc_3 can be obtained via this way in functional programming:
const _ = require('ramda') // requiring ramda as _
function sum(a,b){
return a+b;
}
const curried_sum = _.curry(sum) // currying function sum(a,b)
const inc_1 = curried_sum(1)
const inc_2 = curried_sum(2)
const inc_3 = curried_sum(3)
console.log('1 increase 1 times is',inc_1(1)) // Output: 1 increase 1 times is 2
console.log('1 increase 2 times is',inc_2(1)) // Output: 1 increase 1 times is 3
console.log('1 increase 3 times is',inc_3(1)) // Output: 1 increase 1 times is 4
So, what just happened?
Okay, so what happened is that when we passed sum to _.curry as a parameter in the function call, it created a new function, which we stored in curried_sum ( See, Ramda respected immutability here ).

Now, this curried_ sum is a function which does the same thing our function sum(a,b) used to do, i.e it also adds two numbers, but it can take one argument at a time!
Meaning, when we call curried_sum(1), then it gives us another function in which the value of a has-been replaced/inlined by 1 ( This is an abstract representation of the process ).
So, this new function, inc_1, when called with an argument b, i.e inc_1(b) would give us the addition of the b with 1. This is what happens when you call inc_1(b).
Another Way (:
Okay, so because of this magical thing called Currying, we get something else really interesting. Let me stop the talk and take you through the walk. ( I know this talk-walk sounds lame (: but it rhymed!!!!! )
// Run the program in repl
const inc_5 = curried_sum(5)
console.log( "Hey! Siri is it true that inc_5(5), curried_sum(5,5) and curried_sum(5)(5) gives the same result? " )
console.log("Siri: I know it might baffle you but you need face it, Yes it is", inc_5(5) === curried_sum(5,5) && inc_5(5) === curried_sum(5)(5) )
How is curried_sum(5,5) working?
Currying transforms a function to accept one argument at a time, It doesn’t mean that it can accept only one argument at a time, it just means that it will even work if you provide it only one argument.

Therefore, when we call curried_sum(5,5) then we get the result 10, because when all the arguments are provided to a curried function at once then it evaluates the function in the same way as if it never was curried, this is why it yeilds a result equal to inc_(5).
How, is curried_sum(5)(5) even working?
This is because the curried_sum(5) returns a function and by doing curried_sum(5)(5) we are immediately invoking it. Hence it becomes similar to calling inc_5(5) but in this case, we are immediately invoking the function, therefore we don’t need a variable to store it!

These types of functions are pretty common and are known as Immediately Invoked Function Expression (IIFE)!
f(a,b,c) -> f(a)(b)(c)
I think now you know what I meant when I said currying transforms a function f(a,b,c) to f(a)(b)(c).

When we curried function sum(a,b) then we transformed it to accept one argument at a time ( although it can take all of them at the same time too). Immediately Invoking the functions returned from curried functions made the sum(a)(b) pattern possible!
Here are some other patterns for you to play with!
const _ = require (‘ramda’)
function sum(a,b,c,d){
return (a+b+c+d)
}
const curried_sum = _.curry(sum)
// different patterns
console.log(curried_sum(1)(2)(3)(4))
console.log(curried_sum(1,2)(3,4))
console.log(curried_sum(1,2,3)(4))
console.log(curried_sum(1)(2,3,4))
// you can try some other patterns too
Why should we use currying?
Currying makes it really easy to re-use existing functions in your code-base to create new functions. It advocates re-using existing functions to create new ones.
This makes your programming experience really delightful and makes code easy to manage!
For example, if inc_1 is not working fine, then you have to debug the inc_1 function itself (if you are not using Currying), as the number of functions would increase ( like inc_2, inc_3 ) then the number of function that could cause error will also increase ( because all of them are independent functions ). This will make your job really hard as a programmer.
But, if you have used Currying then you just need to debug the sum(a,b) function ( i.e only one function ) in case of an error. It makes your code reliable and buys you more time!

Thanks!
This was my small introduction to Currying for you, If you want to plunge deep into it and want to know how the wheel itself is made, then go to a magical place known as the internet (shhh! It’s a secret), there lies your answer!
Thanks, for taking out the time to go through this workshop of mine, It makes me really happy when I can teach people something new and interesting. Thanks once again!

If you have any doubts or queries regarding this workshop then reach out to me on Hack Club's Slack, My username is Harsh Bajpai!

